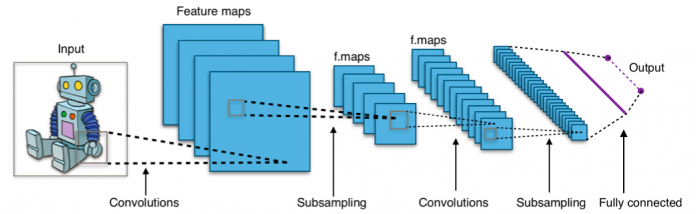
Les réseaux de neurones à convolution sont les véritables superstars des réseaux de neurones. Ces réseaux sont capables d’accomplir des tâches relativement complexes en exploitant des données de type image, son, texte, vidéo etc. Les premiers réseaux de convolution à succès ont été mis au point à la fin des années 90 par le professeur Yann LeCunn pour les laboratoires Bell.
Dans les problèmes de classification style MNIST, on peut utiliser, des perceptrons multicouches qui fournissent de très bons résultats et le temps d’entrainement reste raisonnable. Cependant pour des bases de données — datatsets — plus importantes avec des images de plus grande taille, le nombre de paramètres du réseau croit très rapidement, ce qui rend l’entrainement plus long, et dégrade les performances du modèle.
Limitations des perceptrons multicouches
Les perceptrons multicouches sont redoutablement efficaces pour résoudre plusieurs catégories de problème : classification, estimation, approximation, reconnaissance etc. Cependant, ces derniers peuvent rapidement s’avérer limités, en particulier avec des données de très grande dimension.
Explosion du nombre de paramètres
On veut créer un réseau de neurones pour réaliser une tâche de classification de type chien ou chat. Le modèle est entrainé sur une base de données — datatset — d’images de taille 420x420px grayscale ; le but étant qu’après entrainement , le modèle soit capable à partir d’une image de dire s’il s’agit d’un chien ou d’un chat. Une première approche serait d’utiliser un perceptron multicouche avec une couche d’entrée comportant par exemple 128 neurones. Puisque chacun des neurones reçoit en entrée les 420×420 pixels et attribue un poids par pixel, on a par neurone 420×420 = 176400 poids, multiplié par les 128 neurones auxquels s’ajoutent finalement 128 biais ; un biais par neurone. Notre tout petit modèle devra donc apprendre plus de 22 millions de paramètres. Cela pour seulement 128 neurones et une couche intermédiaire. Si on veut un modèle performant, il faudra plusieurs couches supplémentaires et plus de neurones par couche. Le nombre de paramètres explose. Par exemple pour un modèle 3 couches — 128 256 1 — on a presque 23 millions de paramètres. Un tel modèle nécessite une énorme quantité de données pour être entrainé, et puisque les paramètres à ajuster sont beaucoup plus nombreux, l’entrainement est plus long et les performances se dégradent; disons-le clairement, même si on disposait d’une puissance de calcul suffisante, il serait impossible d’entrainer ce correctement ce modèle, d’autant plus que ce n’est pas le seul problème.
Dégradation spatiale de l’image
Entrainer un perceptron multicouches requiert de lui fournir les données sous forme de vecteur autrement dit, une colonne. Si la donnée d’entrée est une image matricielle, alors il faudra l’aplatir de sorte à obtenir une colonne. Seulement, dans une image, il existe des liens très forts entre pixels voisins; en aplatissant l’image, on perd ces informations, il devient plus difficile pour le réseau d’interpréter les données pendant la phase d’entrainement. Cela justifie qu’on s’intéresse à une autre architecture de réseau de neurones pour résoudre ce genre de problème. Commençons par présenter en quoi consiste une convolution.
Opération de convolution
La convolution est une opération qui permet d’appliquer un filtre — on dit aussi noyau— à une image pour en extraire certaines caractéristiques. Littéralement, on utilise le filtre pour “filtrer” l’image afin de n’afficher que ce qui nous intéresse. L’image considérée est une image matricielle, les filtres sont aussi des matrices, en général 3×3 ou 5×5. Voyons comment faire une convolution avec le noyau suivant,

On dispose d’une matrice 6x6px; on place le noyau de convolution, c’est-à-dire la matrice 3×3 ou 5×5 sur le coin haut de la matrice image, le noyau recouvre alors une partie de la matrice image, on fait un produit élément par élément des deux blocs superposés, on somme ces produits et le résultat final est un pixel de l’image de sortie.
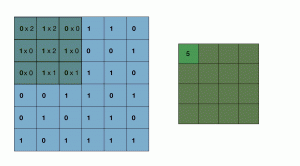
Ensuite, on décale le noyau de convolution d’une case horizontalement — stride en anglais — vers la droite, on fait à nouveau le produit élément par élément puis la somme pour obtenir un nouveau coefficient. Une fois en fin de ligne le noyau descend d’une case verticalement — stride vertical — et repart de la droite, on procède ainsi jusqu’à parcourir toute la matrice image. Il est important de noter que le noyau reste sur la matrice initiale, sans déborder.
Bien sûr, on ne peut pas utiliser n’importe quel filtre, les coefficients de notre noyau vont dépendre des caractéristiques qu’on veut faire ressortir. Voyons le résultat d’une convolution avec quelques filtres connus.
Filtre de Sobel vertical
Il a pour action de mettre en évidence les contours verticaux de l’objet. Appliqué à notre image initiale à gauche, on a le résultat suivant ,

Filtre de Sobel horizontal
Cette fois ce sont les contours horizontaux qu’on va faire ressortir. Voici le résultat si on l’applique à notre image de gauche,

On peut combiner les actions de ces filtres pour réaliser des opérations plus complexes. Il existe ainsi plusieurs filtres déjà répertoriés qu’on peut directement utiliser en fonction de la tâche à résoudre : filtre de moyenne, filtre de Gauss etc. Avant l’émergence du Deep Learning, ce sont des experts humains qui devaient calculer et rechercher les bons filtres permettant de réaliser des actions précises de traitement d’image : détection de parties du visage, montage, retouche photo, filtres Snapchat, etc. Désormais avec le Deep Learning, le calcul de ces filtres se fait par apprentissage automatique, le modèle trouvera en fonction du problème à résoudre, les bons filtres à partir des données d’entrainement. Dans un problème de classification chien ou chat par exemple, les filtres permettront de faire ressortir les caractéristiques déterminantes pour la classification : formes des oreilles, forme des yeux, forme du museau, contour, etc.
Les réseaux de neurones de convolution
Les réseaux de neurones de convolution, pour Convolutional Neural Networks, CNNs, utilisent le principe de la convolution présenté ci-dessus pour réaliser des modèles permettant de résoudre une grande variété de problème à partir de données d’entrainement. Voyons dans le détail un réseau de convolution dans un problème de classification.
Approche des réseaux de neurones
Dans notre problème de classification, nous avons deux catégories, chien et chat. Pour classer une image dans l’une des catégories, il suffit de rechercher dans l’image des caractéristiques singulières, forme du crâne, forme des oreilles, forme des yeux, etc. Dans notre image, seules ces caractéristiques nous intéressent, les autres informations sont peu importantes pour nous. L’idéal serait donc partant d’une image, de pouvoir extraire les caractéristiques intéressantes pour notre problème en utilisant les filtres adéquats, c’est notre modèle qui va déterminer ces filtres. Dans un réseau de convolution, le noyau est initialisé avec des valeurs aléatoires, pendant l’entrainement, ces valeurs seront actualisées par rétropropagation du gradient. Puisqu’il s’agit d’un modèle de DeepLearning, on devine qu’on va empiler plusieurs couches de convolution pour avoir un réseau plus performant.
Padding et effet de bord
On reprend l’exemple de la convolution ci-dessus ; regardons les dimensions de l’image obtenue. L’image initiale est une matrice 6x6px, le filtre est de taille 3×3 on constate que l’image finale — on dit aussi feature map — est de taille 4x4px. En fait, de façon générale, la dimension de l’image finale est :
![]()
où n est la dimension de l’image initiale et p celle du noyau. Par exemple, pour une image initiale au format 120x120px et avec un noyau 5×5, l’image de sortie — feature map — est de taille 116x116px. On voit donc que la convolution réduit la taille de notre image. Si on veut obtenir une image de même dimension que l’image initiale, il faut rajouter des zéros autour de la matrice initiale avant la convolution, on dit qu’on fait un padding. Regardons un exemple.
Cas de la matrice 6x6px avec un noyau 3×3 . On veut que l’image après convolution ait les mêmes dimensions que l’image initiale, soit 6x6px avec un noyau de convolution 3×3. Dans l’équation précédente on a donc p=3, m=6 et il vient alors n =6+3–1 = 8. Ainsi, il faut en entrée une image taille 8x8px, cela signifie qu’il faut rajouter des zéros tout autour de la matrice initiale pour aboutir à une taille de 8x8px; d’où la matrice suivante,
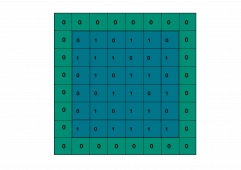
Le padding n’est pas obligatoire et, il arrive généralement qu’on fasse sans ; il peut sembler anecdotique mais il a une réelle utilité. Analysons les pixels du coin supérieur par exemple, ils voient passer le noyau de convolution une seule fois, alors que la plupart des autres pixels le voient plus de deux fois. Les pixels du bord auront donc moins d’influence sur ceux de l’image de sortie. C’est pour limiter cet effet de bord, qu’on augmente la matrice initiale avec des zéros, de sorte que les pixels aux extrémités ne soient pas sous-représentés.
Fonction d’activation
Pendant l’entrainement, on sait que les coefficients de notre filtre sont mis à jour; ceux-ci peuvent être négatifs comme on l’a vu plus haut pour le filtre de Sobel, on comprend alors que les coefficients de la matrice de sortie — feature map — peuvent prendre de grandes valeurs négatives. Puisqu’on sait que ces valeurs représentent des niveaux de pixels, donc positifs, on peut appliquer une fonction pour remplacer les valeurs négatives par des zéros et garder les valeurs positives en l’état. C’est une fonction d’activation appelée fonction relu. Mais il faut garder à l’esprit qu’il existe d’autres fonctions d’activations, l’idée étant sensiblement la même qu’avec relu.
Couche de convolution
On sait désormais que pour faire une convolution, on applique un filtre à une image d’entrée, on obitent alors une feature map qui fait ressortir des caractéristiques — features en anglais — de notre image; contour, ligne, trait, forme etc. Chaque filtre a une tâche simple et précise à realiser. Pour résoudre notre problème de classification, il nous faudra donc associer plusieurs filtres ; et en combinant les caractéristiques ressorties par ces filtres ; forme des oreilles, des yeux, contours, notre modèle pourra s’entrainer à distinguer un chien d’un chat. Il nous faudra donc choisir le nombre de filtre à utiliser, en sachant que plus on aura de filtres, plus nombreux seront les détails extraits pour faire la classification, plus nombreux donc seront les paramètres mais plus performant sera notre modèle. Ensuite, il faut décider si oui ou non on veut faire du padding et enfin, choisir quelle fonction d’activation utiliser. On définit ainsi une couche de convolution. Combien de filtres ? 64, 128, 256 … Quelle fonction d’activation ? relu, sigmoid, tanh… Avec ou sans padding ? Prenons le cas d’une couche de convolution avec 128 filtres par exemple; elle fournit une feature map par filtre et donc 128 feature maps au total pour une image. Ces feature maps représentent différentes informations contenues dans l’image, on peut donc les voir comme différents canaux de cette image. De même qu’une image RGB contient trois canaux (rouge, vert et bleu), une couche de convolution avec 128 filtres fournit une seule image en sortie mais avec 128 canaux. Si la même image repasse par une autre couche de 256 filtres, elle aura en sortie 256 canaux et ainsi de suite. Donc voilà, un réseau de convolution est constitué d’un empilement de couches de convolution. Mais pas que.
Le pooling
Dans une image, il existe une forte corrélation locale entre pixels. Ça signifie que sur une image, si vous savez qu’un pixel est rouge, il est fort probable que ses quatre plus voisins pixels soient aussi des teintes de rouge. Dans le cas d’une image grayscale, si un pixel a une intensité de 180 par exemple, ses pixels les plus voisins auront aussi des intensités autour de 180. Il est donc possible de réduire les dimensions de l’image en ne gardant qu’un représentant local par bloc de pixel, on dit qu’on fait du pooling. En général, on prendra le pixel qui a l’intensité maximale dans le bloc — max pooling — , on peut aussi faire la moyenne des intensités , average pooling.
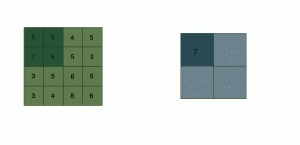
Comme on peut le constater, le pooling divise par deux les dimensions de l’image. On pourrait penser que le max pooling dégrade fortement notre image ; mais en fait non, l’image obtenue est certes deux fois moins grande, mais elle contient les caractéristiques essentielles de l’image initiale.
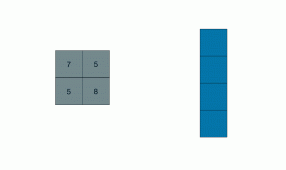
Example d’application du max pooling à la feature map fournie par le filtre de Sobel horizontal, les deux images de droite ont étés agrandies pour la comparaison.

On peut voir, qu’après deux poolings, les contours sont bien visibles et l’image est moins riche en details. Il ne s’agit pas seulement de redimensionner, le pooling permet aussi de garder uniquement les caractéristiques prédominantes de l’image.
Typiquement, dans un réseau de convolution, on a un enchainement d’opérations ; couche de convolution-pooling-couche de convolution-pooling et ainsi de suite. Après avoir effectué ces opérations un certain nombre de fois, on obtient des feature maps ne comportant que les caractéristiques essentielles de l’image d’entrée. On peut maintenant exploiter la puissance d’un perceptron multicouche pour achever de faire la classification.
Aplatir l’image pour la classification finale
Pour classer l’image dans une catégorie, chien ou chat, on va monter un perceptron multicouche (Multi-Layer Perceptron) à la fin les opérations de convolution et pooling. Ces opérations ont permis de réduire grandement les dimensions de l’image pour ne garder que les informations déterminantes pour la classification. Le réseau MLP reçoit donc des features map de petite dimension sous forme de colonne et choisit la catégorie correspondante.
 A présent vous savez tout sur les réseaux de neurones de convolution, si vous souhaitez aller plus loin, vous pouvez lire le paragraphe suivant.
A présent vous savez tout sur les réseaux de neurones de convolution, si vous souhaitez aller plus loin, vous pouvez lire le paragraphe suivant.
Approche plus technique de la convolution
Dans la précédente description, on dit que la convolution est le produit d’une matrice glissante et de la matrice image fournie en entrée. Bien que cette approche soit la plus vulgarisée, on peut l’améliorer sans trop de complexité. Reprenons l’exemple de notre première convolution avec un noyau 3×3 et une matrice 6x6px. On utilise la formule au-dessus pour prévoir la dimension de la feature map— image de sortie — 4x4px.
Le pixel (1, 1), supérieur gauche de la feature map dépend directement des valeurs de pixels dans l’image d’entrée et aussi des valeurs de coefficients du noyau. La valeur de ce pixel est,
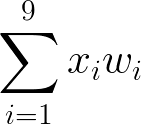
où les wi sont les coefficients du noyau de convolution et les xi, les coefficients de la matrice dans le cadre vert. On rappelle le noyau de convolution,

Ci-dessus, on a par exemple w1=w2=w5=2 et w9=1 et aussi, x1=0, x2=1, x5=1. Dans l’expression du pixel (1, 1), on a une somme pondérée. C’est comme si on avait un neurone où les xi étaient les entrées et les wi coefficients du noyau, les poids des entrées. Le neurone calcule la somme pondérée qui vaut alors la valeur du pixel, ici 5. La zone encadrée est appelée champ réceptif du neurone; en vert le champ réceptif du neurone en position (1, 1) de la feature map.
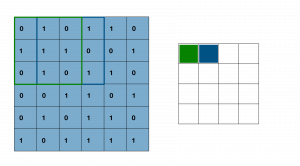
Lorsque le noyau parcourt l’image d’entrée, les valeurs de xi changent mais les poids wi du noyau restent les mêmes. Lors de l’entrainement du réseau, ce sont ces coefficients wi qui sont mis à jour par rétropropagation du gradient. En particulier, tous ces neurones partagent les mêmes poids wi — qui sont les coefficients du noyau de convolution— parce qu’ils recherchent dans l’image les mêmes caractéristiques, par exemple la présence d’un œil. On peut également leur ajouter un biais partagé b, shared bias. La fonction d’activation décrite plus haut est en fait appliquée à ces neurones.
Comme on peut le constater, le champ réceptif du second neurone recouvre en partie celui du neurone précédent et ainsi de suite. Puisque les champs réceptifs de ces neurones se chevauchent, si la caractéristique recherchée est translatée — vers le haut, le bas, la gauche ou la droite — , elle sera forcément dans le champ réceptif d’un autre neurone, donc détectée par ce dernier. On dit qu’on a une invariance par translation. Sans rentrer dans trop de complexité, des travaux de biologie menés dans les années 60 ont permis d’identifier la même structure dans le cortex visuel de certains animaux. En particulier, les premières cellules qui interviennent dans le processus de vision vont identifier des formes géométriques très simples : trait, arrondi, arrête, etc. Des cellules plus complexes vont alors exploiter ces informations pour identifer un motif complet. De même, dans les réseaux de neurones de convolution, les premiers filtres vont détecter des formes géométriques générales : coin, arrondi, arrête, contour etc. Les couches suivantes, combinent alors ces éléments pour identifier des formes plus spécifiques : crâne, œil, oreille etc.
Partant de la formule au-dessus, on sait qu’une convolution sur une image de taille nxn avec un filtre de taille pxp, produit — sans padding — une feature map de taille mxm ; sachant que chaque pixel de la feature map est lié à un neurone, on utilise alors m**2 neurones et chacun d’eux observe un champ de taille pxp avec p**2 poids et un biais. Puisque ces paramètres sont partagés, on a au final p**2 + 1 paramètres pour les m**2neurones. Par exemple, avec une image de 420x420px et un noyau de taille 5*5 on aura m = 420–5+1 = 416 et donc 416*416 = 173056 neurones ! avec seulement 26 paramètres à apprendre.
C’est là, tout l’intérêt des réseaux de neurones de convolution. Pour effectuer une convolution, autrement dit, détecter un motif, les neurones partagent les mêmes poids synaptiques et éventuellement un biais, ce qui réduit grandement le nombre de paramètres à apprendre.
Conclusion
L’objet de cet article était d’introduire les réseaux de neurones de convolution avec leur intérêt majeur. De façon générale, ces réseaux fournissent d’excellents résultats pour les problèmes de classification et de reconnaissance. Ils s’utilisent aussi pour interpréter des données de type son, texte et vidéo. Si le problème à résoudre consiste à rechercher un motif dans une séquence, alors les réseaux de convolution seront de bons candidats. Dans un prochain article, nous allons examiner dans le détail comment les couches successives du réseau de convolution évoluent pendant la phase d’apprentissage, nous verrons aussi comment faire parler ces réseaux à l’aide de Heatmaps.