Ce tutoriel est consacré à la modélisation et l’évaluation de modèles de séries temporelles. Il s’agit de la 3ème partie de notre série consacrée aux séries temporelles. Les séries temporelles sont employées dans de nombreux domaines : finances, marketing, industrie, maintenance pour ne cite qu’eux, principalement à des fins d’analyse prédictive.
Rappelez-vous, nous avions présenté les différentes étapes de l’analyse de séries temporelles, puis nous nous étions penchés plus spécifiquement sur la préparation et l’exploration des données. C’est donc en toute logique que dans cette troisième partie de tutoriel sur l’analyse de séries temporelles, nous allons aborder la modélisation et l’évaluation des données.
Nous continuons notre analyse des séries temporelles avec l’exemple de l’ensemble de données ‘airline passengers’ sur lequel nous avons commencé à travailler lors de l’article précédent.
Dans cette partie vous allez apprendre comment prédire les valeurs futures d’une série temporelle à l’aide d’un modèle linéaire de décomposition. C’est peut-être le type de modèles le plus important en séries temporelles c’est pourquoi nous détaillerons le code.
Puis dans une deuxième partie, les résultats seront critiqués. Le modèle linéaire entraîné précédemment sera comparé avec une prédiction dite naïve, très simple, qui sert de jauge.
Nous ferons tout ceci en R avec les packages dplyr, ggplot et Ecdat.
Modélisation de série temporelle
Il y a plusieurs façons de prédire une série temporelle, nous allons ici employer une méthode de décomposition. C’est une méthode qui a l’avantage d’être rapide à entraîner, d’être interprétable et qui s’applique à de nombreuses situations variées.
Le concept de cette méthode est de simplifier au maximum la série initiale, en procédant à des transformations successives. Une fois la série simplifiée on utilise un algorithme de machine learning, ici on utilisera un modèle linéaire. La dernière étape consiste à inverser les transformations pour remettre les prédictions dans le même contexte que la série initiale.
Décomposition
Dans notre exemple nous utiliserons :
- Une transformation de stabilisation de la variance : une simple application de la fonction logarithmique.
- Une transformation qui enlève la tendance croissante : une différenciation simple.
- Une transformation qui enlève la périodicité annuelle : une différenciation d’intervalle 12 points pour les 12 mois de l’année.
Lors du précédent article nous avons déjà effectué les 2 premières transformations, nous pouvons réutiliser ces résultats et appliquer la dernière :
AirPassengers_finale = diff(AirPassengers_Stab, 12)
Voici un graphe de la série obtenue :
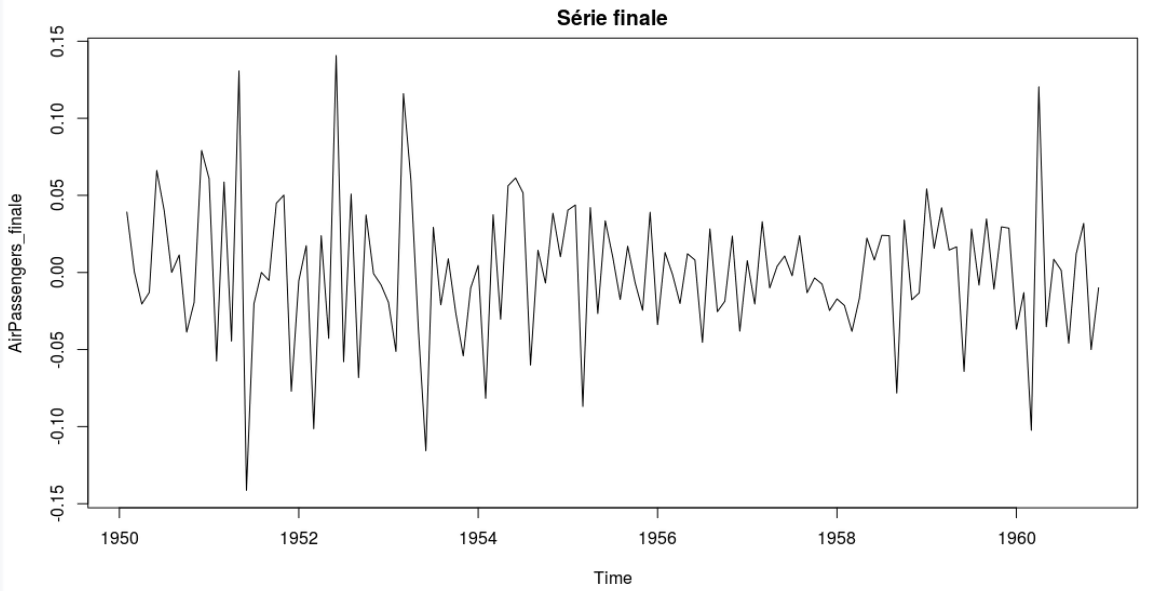
On remarque que cette série n’a plus d’éléments distinctifs évidents, elle ressemble à un bruit. C’est bien le but de l’opération. C’est sur cette série que l’on va entraîner une régression linéaire.
Codage du modèle
On va modéliser la série précédente, que l’on noterapar un processus de type auto-régressif. Ce type de processus est défini par une relation du type:
Où t est la variable de temps, E(t) est un terme d’erreur (techniquement bruit blanc), les lettres a,b… sont des coefficients à déterminer, et k est l’ordre du processus. Ici on choisira k=3. Nous avons donc un modèle qui se réduit à :
Et l’on va estimer les paramètres a, b et c à l’aide d’une régression linéaire.
Voici le code qui permet d’entraîner notre modèle :
decompo_mod <- function(serie_initiale) {
# on initialise un objet qui contiendra les données de notre modèle
model_obj = list()
class(model_obj) <- ‘decompo_mod’
# stabilisation de la variance
serie_VarStab = log(serie_initiale)
# correction de la tendance croissante
serie_stab = diff(serie_VarStab)
# correction de la périodicité annuelle
serie_finale = diff(serie_stab, 12)
# on entraîne le modele auto-regressif
regression_data = data.frame(
y = serie_finale,
y_l1 = lag(serie_finale, 1),
y_l2 = lag(serie_finale, 2),
y_l3 = lag(serie_finale, 3)
)
# les 3 premières lignes contiennent des NAs à cause de la fonction lag
# on les enlève:
regression_data = tail(regression_data, -3)
# on entraîne le modèle auto-régressif linéaire
model_obj$auto_reg = lm(data = regression_data, y ~ 0 + y_l1 + y_l2 + y_l3)
return(model_obj)
}
Et voici le code qui permet de générer les prédictions :
predict.decompo_mod <- function(model, serie_initiale) {
# stabilisation de la variance
serie_VarStab = log(serie_initiale)
# correction de la tendance croissante
serie_stab = c(NA, diff(serie_VarStab))
# correction de la périodicité annuelle
serie_finale = c(rep(NA, 12), diff(serie_stab, 12))
# formattage des données pour le modèle auto-regressif
regression_data = data.frame(
y_l1 = lag(serie_finale, 1),
y_l2 = lag(serie_finale, 2),
y_l3 = lag(serie_finale, 3)
)
pred_lm = predict(model$auto_reg, regression_data)
# on re-périodise la série
serie_pred_periodique = pred_lm + lag(serie_stab, 12)
# on ré-integre la tendance
serie_pred_tendance = serie_pred_periodique + lag(serie_VarStab)
# on inverse la transformation de variance
serie_pred_sortie = exp(serie_pred_tendance)
return(serie_pred_sortie)
}
Finalement on utilise notre modèle pour générer des prédictions :
model <- decompo_mod(c(AirPassengers))
pred <- predict(model, c(AirPassengers))
Notre modèle génère donc des prédictions de séries temporelles ! Mais sont-elles de qualité ? C’est ce que l’on va explorer dans la partie suivante.
Évaluation de notre modèle de prédiction de série temporelle
Nous allons présenter deux outils pour apprécier la qualité d’une prédiction : un graphe et une prédiction naïve jauge.
Notons que notre modèle ne prédit que un pas en avance. Ici un pas correspond à un mois. Nous allons donc étudier la précision de notre prédiction au mois prochain.
Graphe prédiction contre vérité
Sans doute l’outil le plus simple mais aussi le plus parlant, il consiste à afficher ensemble les valeurs originales et les valeurs prédites en fonction du temps. Pour nous voici ce que cela donne :
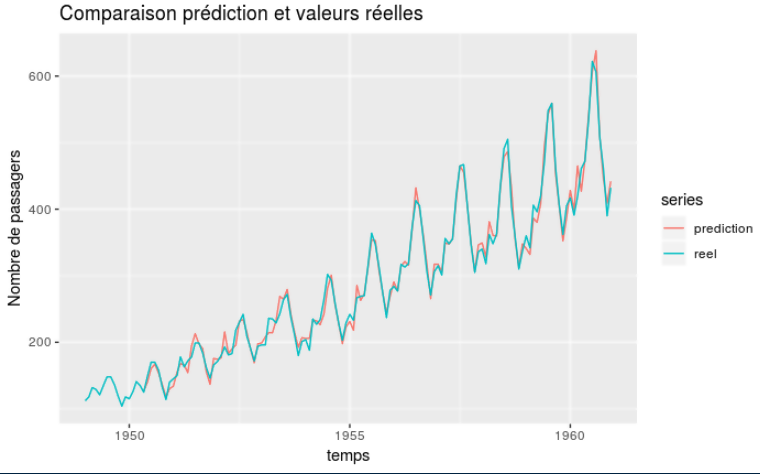
Le modèle semble donc a priori donner des résultats cohérents comme le suggère la proximité des deux courbes.
Modèle naïf
Si l’on veut maintenant quantifier les résultats, on peut utiliser une mesure d’erreur, par exemple l’erreur absolue moyenne (MAE).
On obtient une valeur de 9.1, comment interpréter ce chiffre ? L’idée est de construire un modèle minimaliste ou naïf qui permet de donner un point de repère. Souvent on utilise la valeur du dernier point pour prédire le point actuel. Sur les données de passagers aériens, cette prédiction naïve donne un MAE de 25. Notre modèle est donc 2.8 fois meilleur.
Toujours commencer par évaluer la performance d’une prédiction naïve avant de se lancer dans des modèles plus complexes. C’est très rapide à produire et guidera vos expérimentations avec les algorithmes plus sophistiqués.
Conclusion
Dans cet article nous avons détaillé un modèle de décomposition. Il consiste à appliquer des transformations pour simplifier sa série temporelle. C’est une méthode très efficace et très générale, son application est omniprésente en analyse des séries temporelles, avec différentes variations.
Pour évaluer la qualité de ses prédictions on se souviendra de comparer avec un modèle naïf.
Ressources
https://otexts.com/fpp3/ Forecasting: Principles and Practice, Rob J Hyndman and George Athanasopoulos

