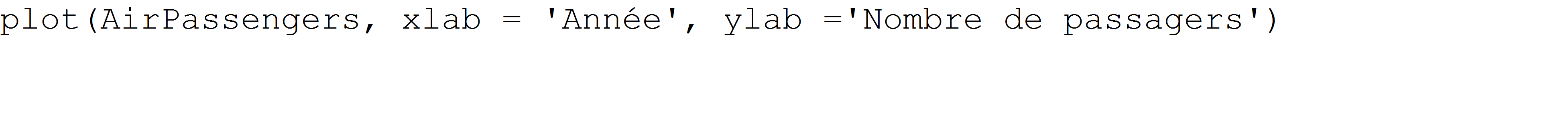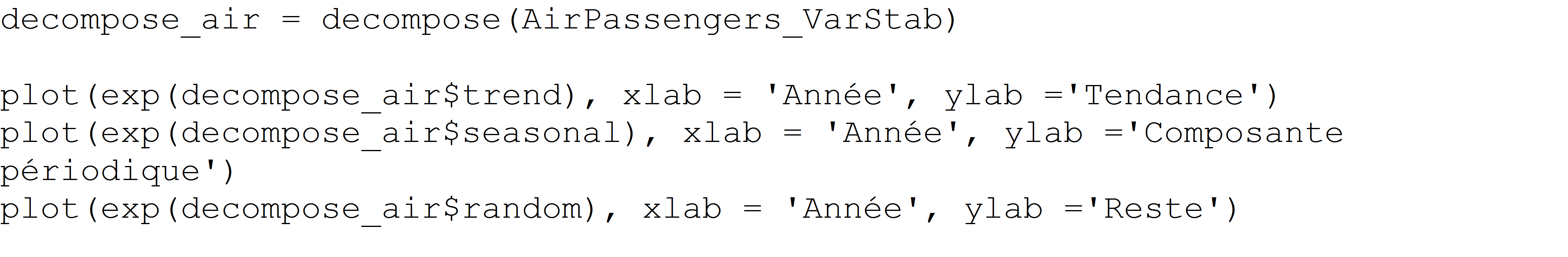Cet article est la 2ème partie de la série de tutoriels consacrée à l’analyse de séries temporelles en intelligence artificielle et science des données. Pour retourner à la première partie (introduction aux séries temporelles) cliquez-ici.
L’exploration des données est l’étape d’analyse qui permet d’évaluer la mise en œuvre de la solution. Ici par des outils de visualisation et de traitement on va essayer d’identifier des caractéristiques comme stationnarité, périodicité et dépendance. Ces caractéristiques vont permettre par la suite de sélectionner une méthode ou algorithme pour répondre au besoin du client.
Mais avant d’explorer ses données il faut les nettoyer! La préparation des données est une partie critique du traitement car toutes les étapes suivantes s’appuieront sur l’ensemble de données produit à ce niveau. Des exemples de problèmes que l’on peut trouver sont des erreurs de hardware, de formatage et de stockages. Ne pas sous-estimer la quantité de données incorrectes, dans le domaine des objets connectés, 30% d’erreurs n’est pas surprenant. On comprend rapidement qu’aucun modèle, aussi sophistiqué soit-il, n’obtiendra de bons résultats avec de tels taux d’erreurs. Ici on s’intéressera aux étapes clefs pour préparer correctement ses séries: gérer la composante temporelle, détecter les mauvaises valeurs et les remplacer.
Préparation
Gérer la composante temporelle
La composante temps a ses propres contraintes techniques: fuseaux horaires, heure d’été et heure d’hiver, différents formats… Toutes ces composantes peuvent possiblement poser problème. Il faut passer le temps nécessaire et visualiser ses données pour s’assurer que ces paramètres sont corrects et constants.
Une bonne technique pour éviter les casses têtes au niveau des formats temporels est de stocker toutes les composantes temps dans un format unique numérique de type ‘timestamp’ dans le même fuseau horaire (typiquement UTC). Ainsi toutes les dates et temps ont un sens clair et non ambigu.
Finalement, on conseille très fortement de régulariser sa série temporelle, c’est-à-dire de rendre tous les intervalles de temps constants. Il y a plusieurs techniques, la plus simple étant d’arrondir la composante temporelle à l’heure, minute ou autre unité la plus proche. Cela donne en général de très bons résultats et évite l’implémentation d’un algorithme d’interpolation.
Enlever les mauvaises données
Ce qui détermine si une valeur est correcte ou non dépend bien évidemment du domaine d’application. Ci-dessous on liste différents exemples de types d’erreurs:
- valeur non physique: par exemple une température d’eau liquide au-dessus de 100°C.
- Valeur exactement constante: une température d’eau mesurée à exactement la même valeur à plusieurs points consécutifs (exemple 23,343°C 5 fois d’affilée). Cela suggère un problème car une valeur physique évolue dans le temps ne serait-ce que dans les centièmes ou les millièmes.
- Valeur aberrante: une valeur physiquement possible mais qui semble trop différente du reste de la distribution pour être correcte. Exemple une seule température à 80°C alors que toutes les autres valeurs sont inférieures à 30°C. Cela peut être défini par un simple seuil ou par un modèle.
- Changement de comportement: La série se comporte différemment à partir d’un certain temps pivot. Cela peut être dû à un changement physique ou une erreur de routage des données. Dans les deux cas il faudra traiter différemment la partie avant et après le pivot.
Une fois qu’on a détecté les problèmes on peut les marquer en créant une nouvelle série temporelle booléenne qui est ‘vrai’ seulement aux instants où les données sont bonnes. Cela peut être implémenté simplement en ajoutant une colonne à la série.
Remplacer les mauvaises données
Une fois qu’on a repéré les mauvaises données on va les remplacer afin d’avoir une série temporelle régulière ‘sans trous’. Je conseille de commencer par un remplacement très simple, par exemple utiliser la moyenne de la série. C’est une méthode temporaire, une fois que vous aurez un modèle de prédiction (étape analyse) vous pourrez vous en servir pour prédire ‘dans le passé’ et remplacer les mauvaises valeurs de façon optimale.
Le travail de préparation ou nettoyage des données est indispensable à toute analyse. Très souvent le client vous demandera même explicitement ce travail pour rendre les données ‘présentables’ dans les visualisations. Contrairement à ce que suggère le mot préparation, il ne s’agit pas d’une étape que l’on fait une fois et qui reste figée. En pratique, on fera évoluer la préparation des données à mesure que l’analyse et la compréhension du problème progresse.
Exploration des données
En ce qui concerne l’exploration des données, on commencera par présenter la stationnarité, concept essentiel en analyse temporelle. Ensuite nous passerons à la décomposition des séries temporelles et finalement l’étude des dépendances pour les analyses multivariées.
Pour illustrer cette partie, nous utiliserons R et l’ensemble de données ‘AirPassengers’ de la librairie ‘Ecdat’. Cet exemple est en partie tiré de l’article (https://machinelearningmastery.com/decompose-time-series-data-trend-seasonality/)

On peut avoir une idée de la série en affichant ses valeurs en fonction du temps.

Stationnarité
La stationnarité signifie que les statistiques de la série temporelle ne dépendent pas du temps. En particulier cela veut dire que il n’y a pas de tendance générale et que les variations apparaissent comme d’amplitude constante. Par exemple, les données du nombre de passagers présentées ci-dessus sont non stationnaires car il y a une claire tendance croissante ainsi que des variations de plus en plus grandes à mesure que le temps avance.
Pour stabiliser les variations au cours du temps on pourra utiliser une transformation de type racine carrée, logarithmique, ou plus généralement une transformation de type Box Cox. (Voir https://machinelearningmastery.com/power-transform-time-series-forecast-data-python/)
Sur notre exemple, une transformation de type logarithmique semble bien fonctionner.


Les outils pour enlever la tendance sont principalement la différenciation, simple ou multiple (voir ce bon résumé https://people.duke.edu/~rnau/411diff.htm).
Ici, on réalise une différenciation simple :


Il est quasiment toujours conseillé de stationnariser sa série avant d’appliquer un modèle de machine learning. Les performances seront en générale bien meilleures.
Décomposition
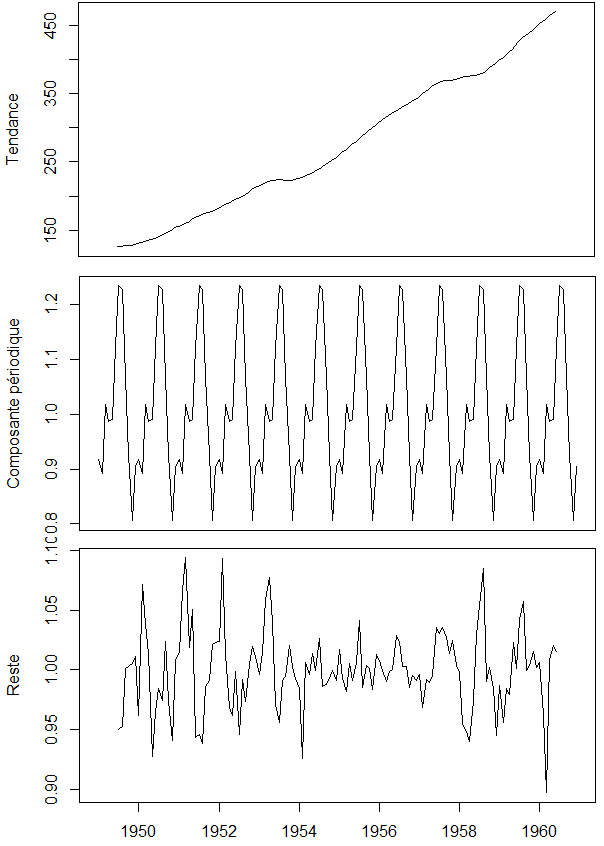
La décomposition d’une série temporelle consiste à séparer sa série initiale en plusieurs sous-séries plus simples, chacune représentant un aspect essentiel de la série initiale. Une décomposition typique est la décomposition en 3 séries: tendance, périodique et reste. On retrouve la série originale si on somme les 3 séries composantes.
Dans le graphe ci-dessous on sépare les composantes de tendance, périodique, et le reste avant de les afficher. Notez que l’on applique la décomposition à la série dont la variance a été stabilisée) afin d’avoir une composante périodique qui reste stable dans le temps. Pour l’affichage, on inverse la transformation logarithmique (avec la fonction ‘exp’) pour avoir les données dans l’unité originale.
Dépendances
Lorsque l’on veut traiter de multiples séries temporelles en même temps on parle de problème multivarié.
Des outils existent comme la covariance croisée, qui permet d’évaluer l’influence d’une série sur l’autre à différents intervalles. Attention cet outil ne peut être utilisé que sur des séries stationnaires. Un autre outil simple consiste à représenter les valeurs d’une série en fonction des valeurs de l’autre sur un graphe de type nuage de point.
Conclusion de cette partie
Dans la préparation, on cherchera à obtenir une série régulière, sans trous, avec des valeurs physiquement cohérentes avec le domaine d’application. Une fois les données nettoyées, on explore les composantes tendances et périodiques de sa série et on cherche à la rendre stationnaire. On est maintenant prêts pour les étapes de modélisation et évaluation que nous allons discuter lors du prochain article.
Accéder à la troisième partie : modélisation et évaluation de séries temporelles