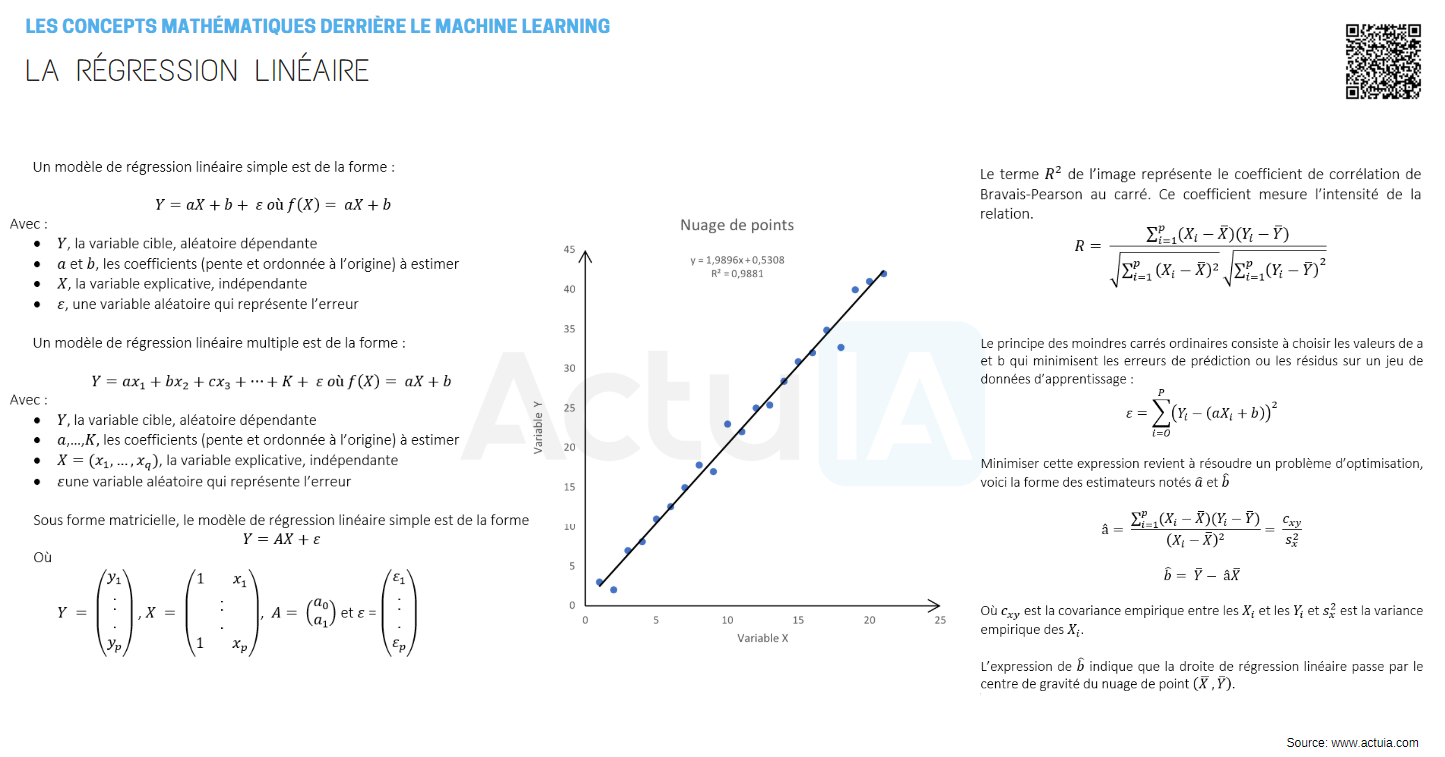
Concepts mathématiques derrière le machine learning : la régression linéaire

Nous avons le plaisir de vous proposer une nouvelle série d’articles consacrée aux concepts mathématiques qui se cachent derrière le machine learning. Nous débutons avec la régression linéaire, un concept relativement simple mais qui peut se réveler dans de nombreux cas suffisant.

Ces dernières années, l’informatique et la programmation sont des domaines d’étude en pleine émergence. Avec l’informatisation des entreprises, les données récoltées sont de plus en plus nombreuses et les questions de stockage et de manipulations de ces données sont des casse-tête pour les mathématiciens et informaticiens. C’est ce qui a fait naître le terme très généraliste de Big Data.

Plusieurs techniques issues de la statistique et de la probabilité ont permis d’accroître les connaissances sur l’analyse de données, la suppression de données aberrantes ou gérer les données manquantes pour choisir une représentation pertinente d’un phénomène. Une fois les données bien préparées, se pose la question de comment tirer des informations efficaces sur des données en grande quantité qui nécessiterait des procédures trop gourmandes en ressources informatiques et des connaissances peu développées.

C’est à ce niveau qu’intervient le machine learning ou l’apprentissage automatique qui permet de rendre un programme capable d’apprendre à partir d’exemple de données sans être programmé. Cette définition du machine learning nous vient d’Arthur Samuel (1959).

L’idée est facile à comprendre, elle est similaire à l’apprentissage d’un être humain qui au bout de plusieurs expériences sur un même sujet devient de plus en plus efficace et autonome.

En pratique, faire apprendre un programme ou un robot nécessite des connaissances en mathématiques, plus précisément les statistiques et probabilités pour construire des modèles et l’informatique pour implémenter des algorithmes efficaces et robustes.

Une fois l’algorithme implémenté, la machine peut apprendre et prédire des phénomènes précis et s’enrichir au fur et à mesure qu’il reçoit de nouvelles données. On peut dorénavant les qualifier de systèmes « intelligents ».
Le machine learning, communément appelé ML devient l’une des branches principales de l’intelligence artificielle, Le machine learning peut-être divisé en plusieurs types de problématiques : l’apprentissage supervisé, l’apprentissage semi-supervisé et l’apprentissage non supervisé. Il englobe notamment le Deep Learning (apprentissage profond), très à la mode.

Nous nous penchons aujourd’hui sur la régression linéaire, l’un des concepts de base du machine learning.

La régression linéaire

L’algorithme de régression linéaire est un algorithme d’apprentissage supervisé c’est-à-dire qu’à partir de la variable cible ou de la variable à expliquer (Y), le modèle a pour but de faire une prédiction grâce à des variables dites explicatives (X) ou prédictives.

Prédire la valeur d’une maison en fonction de sa superficie, sa localisation, la possibilité de parking ou non, prédire le nombre d’utilisateurs et utilisatrices d’un service en ligne à un moment donné sont deux exemples d’utilisation du modèle de régression linéaire.

Voyons ensemble à quoi ressemble le modèle de régression linéaire.

Un modèle de régression linéaire est un modèle de machine learning dont la variable cible (Y) est quantitative tandis que la variable X peut être quantitative ou qualitative.

L’objectif est de trouver une fonction dite de prédiction ou une fonction coût qui décrit la relation entre X et Y c’est-à-dire qu’à partir de valeurs connues de X, on arrive à donner une prédiction des valeurs de Y.

La fonction recherchée est de la forme :

Y= f(X) avec
f(X) une fonction linéaire

À partir d’un échantillon de population qui représente nos données, on répartit les données en deux groupes, les données d’entraînement et les données de test. La première catégorie de données servira pendant la phase d’apprentissage du modèle alors que le second sera utilisé pour évaluer la qualité de prédiction du modèle. Le but n’est donc pas de construire une fonction qui prédira avec une précision optimale les valeurs des variables cibles mais une fonction qui se généralisera au mieux pour prédire des valeurs de données qui n’ont pas encore été observées.

Avant de débuter une étude de régression simple, il faut d’abord tracer les observations .(X_i , Y_i ), i=1,…,p

1) Représentation graphique

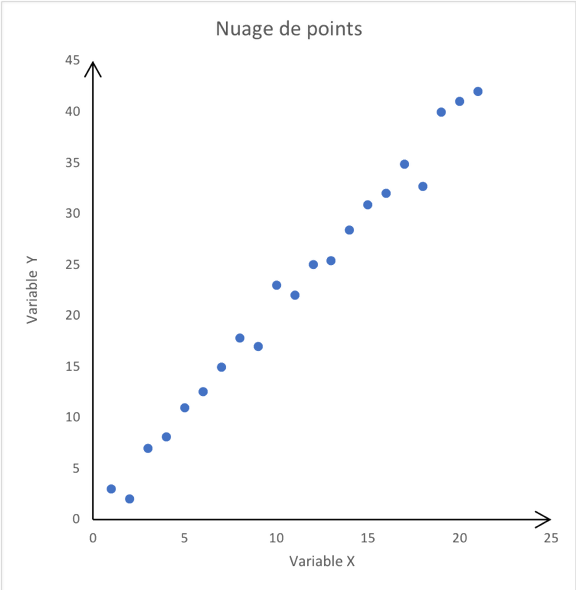
Le but est de savoir si le modèle linéaire est oui ou non pertinent pour l’étude de notre phénomène. Le graphique est au départ un nuage de points et on relève la tendance qu’a la forme de ce nuage de points.

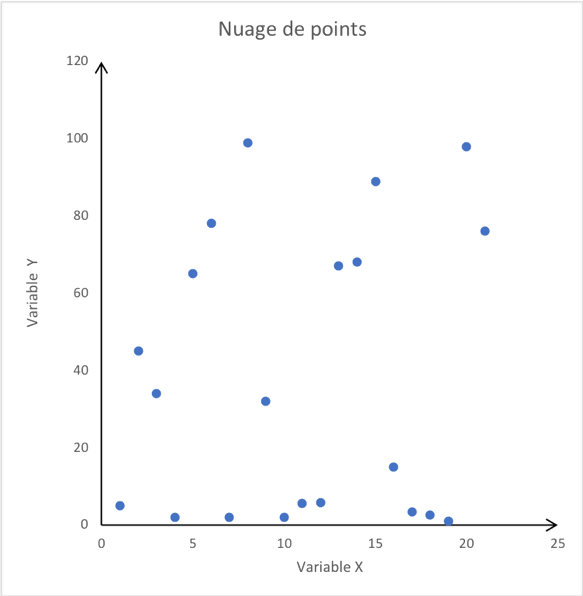Au vu de ces deux graphiques, il semble approprié d’utiliser le modèle linéaire pour la première image et pas pour la deuxième qui ne laisse transparaitre aucune tendance connue.

Dans la suite nous expliquerons la modélisation et l’estimation des paramètres de la fonction de prédiction pour pouvoir tracer cette droite.

2) Modélisation

2.1) Modèle de la régression linéaire

Modélisation	Nature de la régression
Une seule variable explicative X	Régression simple
Plusieurs variables explicatives *X_j (j=1,…,q)*	Régression multiples

Le modèle de régression linéaire analyse les relations entre la variable dépendante ou variable cible Y et l’ensemble des variables indépendantes ou explicatives X. Cette relation est exprimée comme une équation qui prédit les valeurs de la variable cible comme une combinaison linéaire de paramètres.

Un modèle de régression linéaire simple est de la forme :

Y=aX+b+ ε où f(X)= aX+b

Avec :

Y, la variable cible, aléatoire dépendante
a et b, les coefficients (pente et ordonnée à l’origine) à estimer
X, la variable explicative, indépendante
ε, une variable aléatoire qui représente l’erreur

Un modèle de régression linéaire multiple est de la forme :

Y=ax₁+bx₂+cx₃+⋯+K+ ε où f(X)= aX+b

Avec :

Y, la variable cible, aléatoire dépendante
a,…,K les coefficients (pente et ordonnée à l’origine) à estimer
X=(x₁,…,x_q), la variable explicative, indépendante
ε, une variable aléatoire qui représente l’erreur

Sous forme matricielle, le modèle de régression linéaire simple est de la forme :

Y=AX+ε

Où

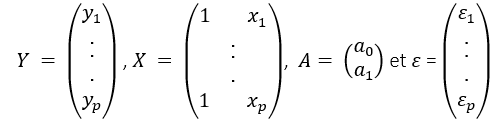
Avec :

Y, un vecteur à expliquer de taille n x 1,
X, la matrice explicative de taille n x 2,
ε, le vecteur d’erreurs de taille n x 1

ε est appelé résidus c’est l’ erreur commise, c’est-à-dire l’écart entre la valeur Y_i observée et la valeur a_iX_i+b donnée par la relation linéaire. En effet, même si une relation linéaire est effectivement présente, les données mesurées ne vérifient pas en général cette relation exactement. Pour ce faire, on tient compte dans le modèle mathématique des erreurs observées.

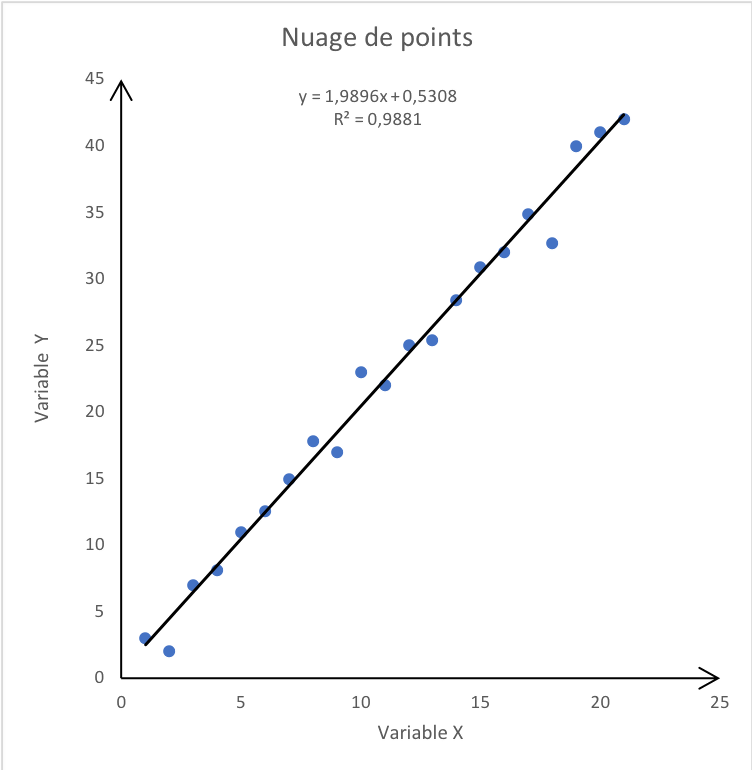
Sur ce graphique, la droite de régression linéaire ou la droite des moindres carrés de Y en X représente la droite d’ajustement linéaire, celle qui résume le mieux la structure du nuage de points pendant la phase d’apprentissage.

Elle rend minimale la somme des carrés des erreurs d’ajustement, nous verrons plus en détail comment minimiser cette erreur dans le prochain paragraphe.

C’est en confrontant l’équation calculée par l’algorithme de régression linéaire aux nouvelles données de la réalité (X) que les prédictions (Y) seront réalisées par l’algorithme d’intelligence artificielle en production.

Le terme R² de l’image représente le coefficient de corrélation de Bravais-Pearson au carré. Ce coefficient mesure l’intensité de la relation linéaire entre Y et X .

Voici sa formule :

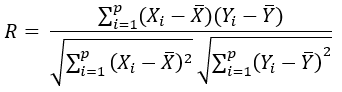
Le coefficient de corrélation est un nombre toujours compris entre -1 et 1.

Si R est proche de 1 : il y a une forte liaison linéaire entre les variables et les valeurs prises par Y ont tendance à croître quand les valeurs de X augmentent.
Si R est proche de 0 : il n’y a pas de liaison linéaire
Si R est proche de -1 : il y a une forte liaison linéaire et les valeurs prises par Y ont tendance à décroître quand les valeurs de X augmentent.

Le coefficient de corrélation mesure la qualité de la droite d’ajustement linéaire mais ne représente en aucun cas une cause de la relation logique entre X et Y. Seul le data scientist pourra estimer de la relation logique entre les deux variables. Exemple : la mortalité des jeunes enfants désespère les femmes qui renoncent à lire Freud… Bien que le coefficient de corrélation soit supérieur à 0, il n’y a aucun lien logique entre les deux phénomènes. Il faut donc faire une distinction entre corrélation et causalité.

2.2) Estimation des coefficients de la droite par la méthode des moindres carrés

La régression linéaire est relativement simple d’un point de vue mathématique. Ce qui fait que ce type d’algorithme entre pleinement dans le cadre de ce que l’on appelle le Machine Learning, ou apprentissage machine, est le fait qu’un logiciel soit capable d’ajuster les paramètres a et b à partir d’exemples fournis par l’utilisateur.

Dans cette partie, nous expliquons comment ces paramètres sont ajustés afin d’estimer la variable de sortie Y.

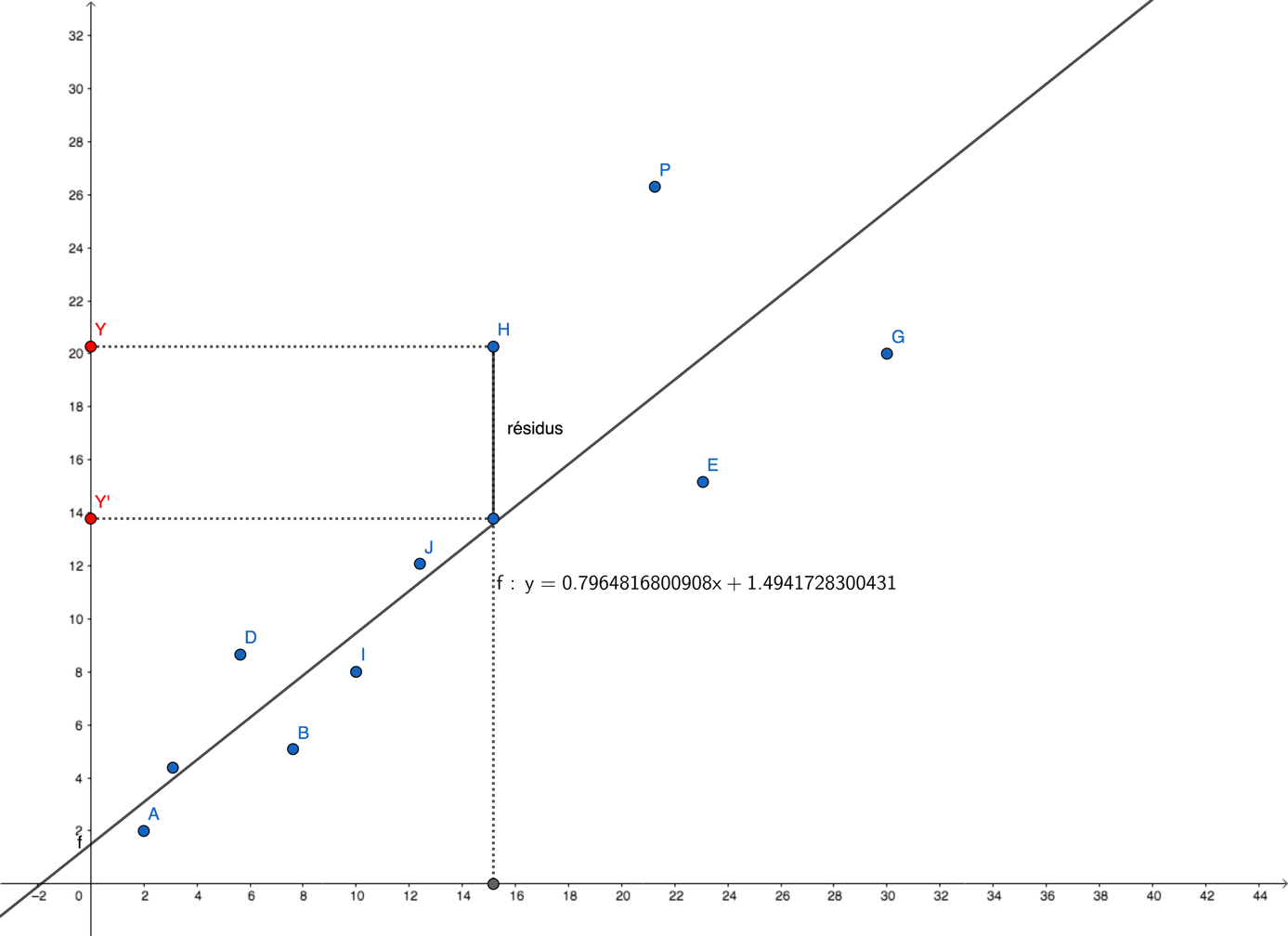
Le principe des moindres carrés ordinaires consiste à choisir les valeurs de a et b qui minimisent les erreurs de prédiction ou les résidus sur un jeu de données d’apprentissage :

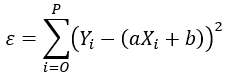
Minimiser cette expression revient à résoudre un problème d’optimisation, voici la forme des estimateurs notés â et b̂ qui sont égaux à

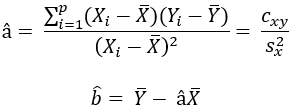
Où c_xy est la covariance empirique entre les X_i et les Y_i et S_x² est la variance empirique des X_i.

L’expression de b̂ indique que la droite de régression linéaire passe par le centre de gravité du nuage de points (X̅,Ȳ).

Conclusion

L’avantage de l’algorithme de régression linéaire est sa simplicité d’interprétation et sa facilité de calcul. Par contre, le data scientist veillera à bien vérifier qu’il existe une relation linéaire entre les paramètres d’entrée et celle de sortie.

Le modèle présente quelques inconvénients comme le fait que l’algorithme est très sensible aux valeurs aberrantes (outliers) des données d’apprentissage d’où la nécessité de bien préparer ses données dès le départ. Il existe des méthodes dites de régularisation pour pallier à ce problème. Les méthodes de régularisation permettent de pénaliser les valeurs trop grandes des coefficients a_i et b.

De plus, le caractère linéaire du modèle néglige les interactions entre les variables explicatives. C’est pour cela qu’il existe une possibilité de définir de nouvelles variables explicatives comme étant le produit de variables existantes.

Nous nous vous proposerons très prochainement un nouvel article sur l’algorithme de la régression logistique.

D’ici là, n’hésitez pas à télécharger/partager notre fiche mnémotechnique (cheat sheet) :