La multiplication matricielle est au cœur de nombreuses tâches de calcul, notamment les réseaux de neurones, les graphiques 3D… DeepMind a présenté récemment AlphaTensor, une approche d’apprentissage par renforcement profond basée sur AlphaZero, « permettant de découvrir des algorithmes nouveaux, efficaces et prouvablement corrects » pour des tâches fondamentales telles que la multiplication matricielle. L’équipe de recherche a publié ses travaux dans l’article « Discovering faster matrix multiplication algorithms with reinforcement learning » début octobre dans la revue Nature.
La multiplication matricielle est l’une des opérations les plus simples en algèbre, couramment enseignée dans les cours de mathématiques du secondaire. En dépit de ce fait, elle sous-tend de nombreux processus dans l’informatique et le monde numérique.
Elle est utilisée pour traiter des images sur des smartphones, reconnaître des commandes vocales, générer des graphiques pour des jeux informatiques, exécuter des simulations, pour prédire la météo, compresser des données et des vidéos pour les partager sur Internet… D’ailleurs, les entreprises du monde entier investissent beaucoup de temps et d’argent au développement de matériel informatique pour multiplier efficacement les matrices. Ainsi, même des améliorations mineures de l’efficacité de la multiplication matricielle peuvent avoir un impact généralisé.
L’algorithme de Strassen
Pendant des siècles, les mathématiciens ont cru que l’algorithme de multiplication matricielle standard était le meilleur que l’on pouvait atteindre en termes d’efficacité. Mais en 1969, le mathématicien allemand Volker Strassen a présenté une méthode pour multiplier les matrices de taille deux plus rapidement que les méthodes standard connues jusque-là. Alors considéré comme révolutionnaire, il est encore souvent utilisé aujourd’hui.
En étudiant de très petites matrices (taille 2×2), Volker Strassen a découvert une façon ingénieuse de combiner les entrées des matrices pour produire un algorithme plus rapide. Plus de cinquante ans après, les experts n’ont pas trouvé l’algorithme optimal pour multiplier deux matrices 3 × 3, pas plus que réussi à surpasser l’approche à deux niveaux de Strassen dans un corps fini, ce qu’AlphaTensor a réalisé.
La figure ci-dessous illustre un tenseur de multiplication matricielle et algorithmes.
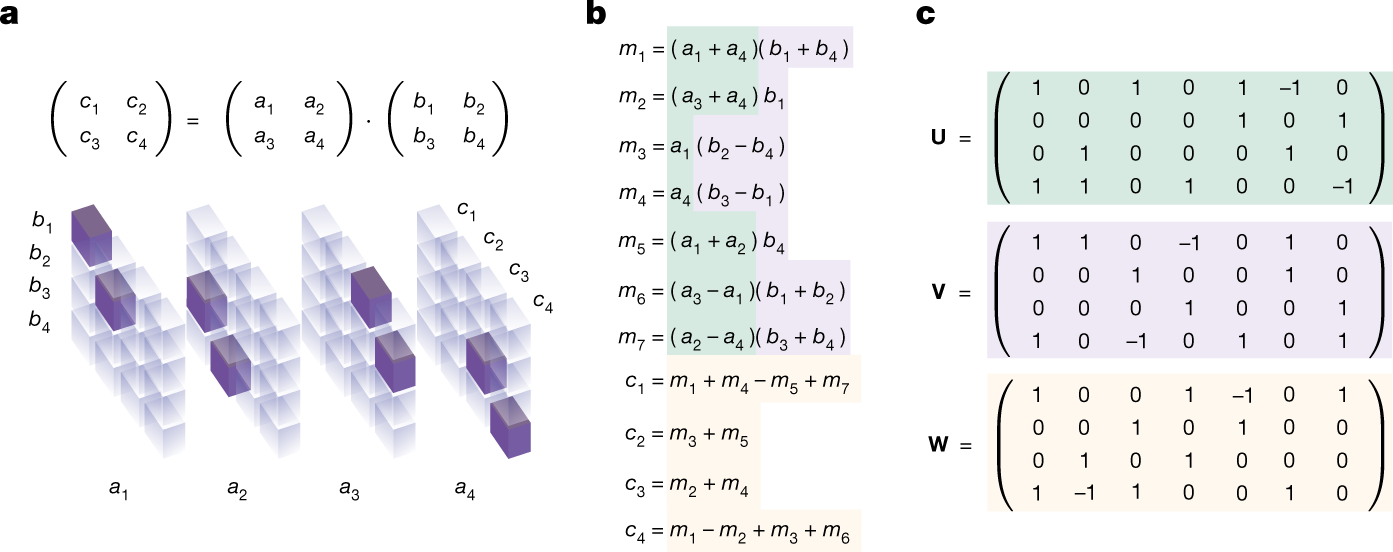
Le jeu solo TensorGame
Les chercheurs ont formulé la procédure de découverte de l’algorithme de multiplication matricielle (c’est-à-dire le problème de décomposition du tenseur) comme un jeu solo, appelé TensorGame. À chaque étape de TensorGame, le joueur sélectionne une combinaison de différentes entrées des matrices pour les multiplier. Un score est attribué en fonction du nombre d’opérations sélectionnées qui ont permis d’atteindre le résultat de multiplication correct. Selon eux, c’est un jeu stimulant avec un énorme espace d’action (plus de 1012 actions pour la plupart des cas intéressants), beaucoup plus grand que celui des jeux de société traditionnels tels que les échecs et le Go qui ne comptent que des centaines d’actions.
L’algorithme AlphaTensor
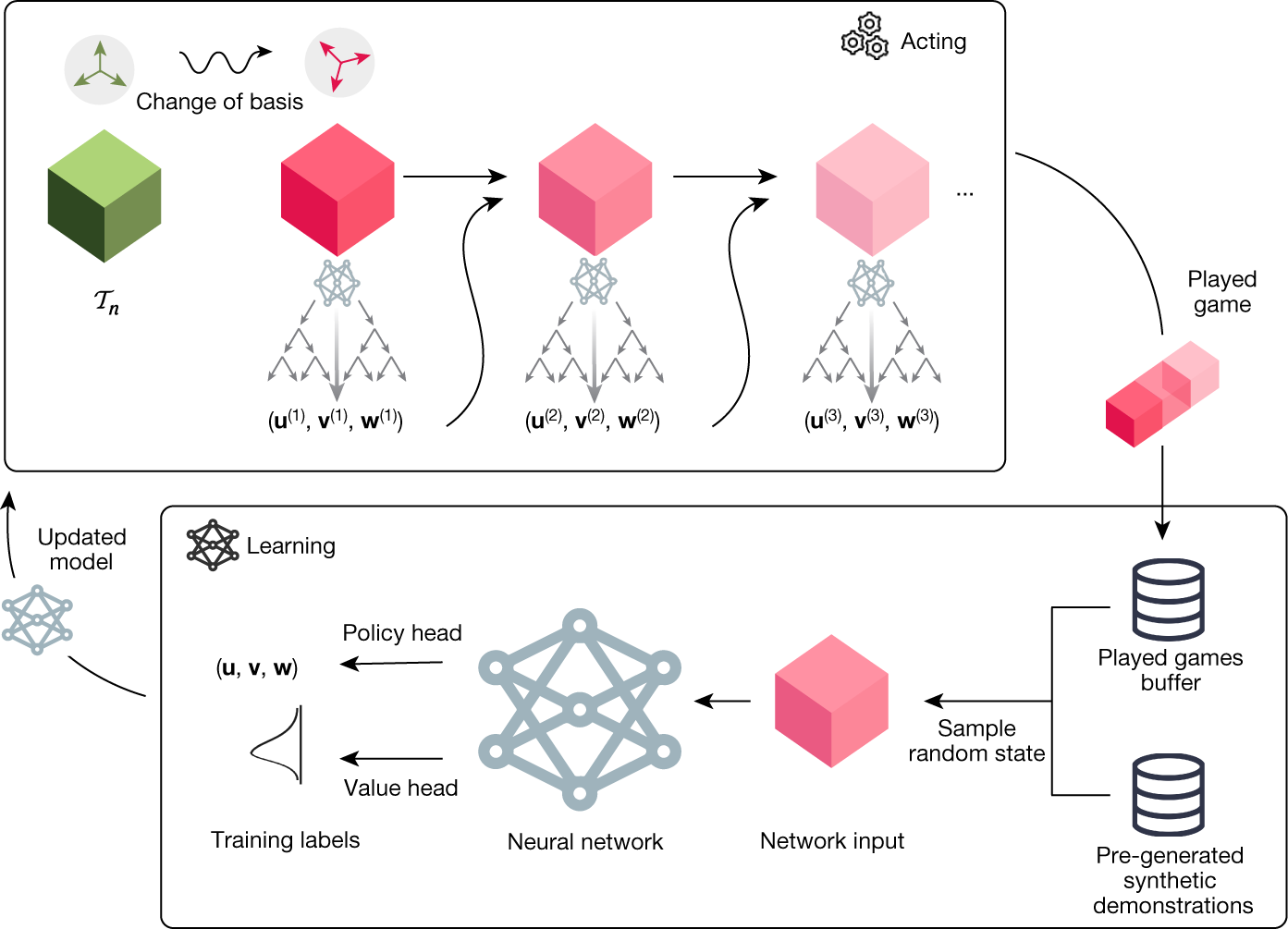
Pour jouer à TensorGame, ils ont proposé AlphaTensor, un agent basé sur AlphaZero et son extension pour gérer de grands espaces d’action Sampled AlphaZero. Comme AlphaZero, AlphaTensor utilise un réseau neuronal profond pour guider une procédure de planification de recherche d’arbres de Monte Carlo (MCTS).
Le réseau prend en entrée un état, c’est-à-dire un tenseur à décomposer, et génère une stratégie et une valeur. La stratégie fournit une répartition sur les actions potentielles.
Résultats
AlphaTensor a découvert des algorithmes qui surpassent la complexité de pointe pour de nombreuses tailles de matrice, notamment pour les matrices 4 x 4 dans un corps fini, où il est le 1er à avoir surpassé l’algorithme à deux niveaux de Strassen, il a en effet découvert une solution en 47 étapes alors que celle de Strassen en comptait 49.
Ces algorithmes de multiplication de petites matrices peuvent être utilisés comme primitives pour multiplier des matrices beaucoup plus grandes de taille arbitraire.
AlphaTensor a permis la découverte d’un ensemble diversifié d’algorithmes avec une complexité de pointe : jusqu’à des milliers d’algorithmes de multiplication matricielle pour chaque taille, démontrant ainsi que l’espace des algorithmes de multiplication matricielle est plus riche qu’on ne le pensait auparavant.
Les chercheurs ont tiré parti de la diversité des propriétés mathématiques et pratiques différentes de ces algorithmes et ainsi adapté AlphaTensor pour trouver spécifiquement des algorithmes rapides sur un matériel donné, tels que le GPU Nvidia V100 et Google TPU v2.
Ces derniers multiplient les grandes matrices 10 à 20 % plus rapidement que les algorithmes couramment utilisés sur le même matériel, ce qui a permis de mettre en valeur la flexibilité d’AlphaTensor dans l’optimisation d’objectifs arbitraires.
Sources de l’article :
« Discovering faster matrix multiplication algorithms with reinforcement learning ».Nature 610, 47-53 (2022). https://doi.org/10.1038/s41586-022-05172-4
Auteurs : Alhussein Fawzi, Matej Balog, Aja Huang, Thomas Hubert, Bernardino Romera-Paredes, Mohammadamin Barekatain, Alexander Novikov, Francisco J. R. Ruiz, Julian Schrittwieser, Grzegorz Swirszcz, David Silver, Demis Hassabis & Pushmeet Kohli

