DeepMind, le laboratoire d’IA de Google, a présenté la semaine dernière AlphaGeometry, un système d’IA développé en collaboration avec le département d’informatique de l’Université de New York. En résolvant des problèmes de géométrie complexes à un niveau comparable à celui d’un médaillé d’or olympique humain, AlphaGeometry représente une étape importante vers le développement de systèmes d’IA plus avancés et plus généraux.
En 2019, une équipe de Google Research avait développé en 2019, DeepHol, un prouveur de théorèmes neuronal basé sur le logiciel HOL Light Theorem Prover, une grande partie des théorèmes étudiés concernaient l’algèbre linéaire. Le prouveur de théorèmes neuronal AlphaGeometry s’adresse à la géométrie plane euclidienne.
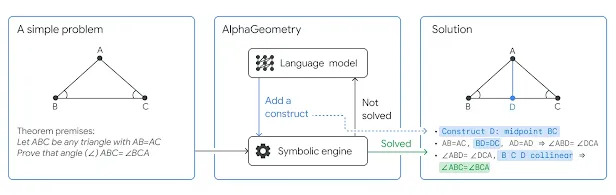
AlphaGeometry adopte une approche neuro-symbolique, combinant un modèle de langage neuronal et un moteur de déduction symbolique. Cette synergie permet à l’IA de générer des idées rapides et intuitives tout en prenant des décisions délibérées et rationnelles. Les modèles de langage excellent dans l’identification de modèles généraux et de relations dans les données, tandis que les moteurs de déduction symbolique utilisent une logique formelle pour parvenir à des conclusions. Ensemble, ils forment un système capable de résoudre des problèmes de géométrie complexes.
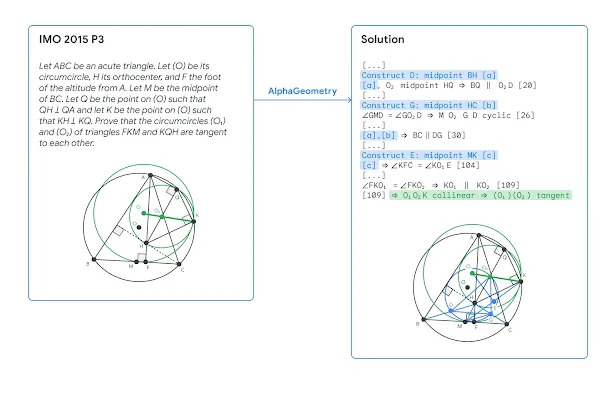
Lors d’un test comparatif portant sur 30 problèmes de géométrie de l’Olympiade internationale de mathématiques (OIM), une compétition mondiale de mathématiques destinée aux élèves des lycées et collèges, AlphaGeometry a résolu 25 problèmes dans les délais impartis, se rapprochant ainsi du score des médaillés d’or humains qui ont résolu en moyenne 25,9 problèmes. En comparaison, le système de pointe précédent, connu sous le nom de “méthode de Wu”, n’avait résolu que 10 de ces problèmes.
L’approche neuro-symbolique
Les problèmes de géométrie des Olympiades sont basés sur des diagrammes qui nécessitent l’ajout de nouvelles constructions géométriques avant de pouvoir être résolus, tels que des points, des lignes ou des cercles.
Le modèle de langage neuronal, entraîné à partir de zéro sur une vaste base de données synthétiques, guide le moteur de déduction vers la solution, comme on peut le voir dans les figures ci-dessous.
Génération de données synthétiques à grande échelle
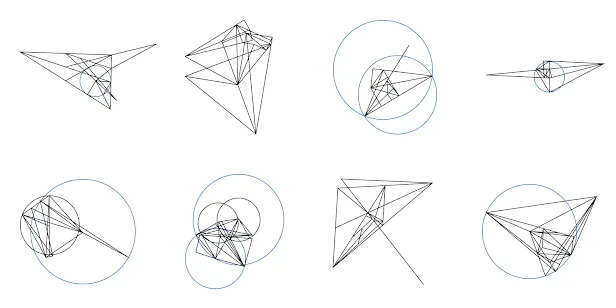
L’un des défis majeurs pour les chercheurs était le manque de données d’entraînement. Ils ont surmonté cette limitation en développant une méthode innovante permettant de générer un milliard de diagrammes aléatoires d’objets géométriques et dériver toutes les relations entre les points et les lignes de chaque diagramme. Un ensemble d’apprentissage de 100 millions d’exemples uniques de difficulté variable a été créé, permettant au modèle de langage de s’entraîner sans aucune démonstration humaine pour prédire les constructions utiles.
L’objectif à long terme de l’équipe de recherche est de construire des systèmes d’IA capables de se généraliser dans tous les domaines mathématiques “en développant la résolution de problèmes et le raisonnement sophistiqués dont dépendront les systèmes d’IA généraux, tout en repoussant les frontières de la connaissance humaine”.
En mettant en open source le code et le modèle d’AlphaGeometry, l’équipe espère encourager le développement d’autres outils et approches pour ouvrir de nouvelles possibilités dans les domaines des mathématiques, des sciences et de l’IA.
Références de l’article :
Blog DeepMind
Article “Solving olympiad geometry without human demonstrations” Nature https://doi.org/10.1038/s41586-023-06747-5
Auteurs et affiliations :
- Trieu H. Trinh, Yuhuai Wu, Quoc V. Le et Thang Luong, Google Research
- He He, professeur adjoint au département d’informatique de l’Université de New York

