Matrix multiplication is at the heart of many computational tasks, including neural networks, 3D graphics… DeepMind recently introduced AlphaTensor, a deep reinforcement learning approach based on AlphaZero, ” to discover new, efficient and provably correct algorithms” for fundamental tasks such as matrix multiplication. The research team published their work in the article “Discovering faster matrix multiplication algorithms with reinforcement learning” in early October in the journal Nature.

Matrix multiplication is one of the simplest operations in algebra, commonly taught in high school math classes. Despite this fact, it underlies many processes in computing and the digital world.

It is used to process images on smartphones, to recognize voice commands, to generate graphics for computer games, to run simulations, to predict the weather, to compress data and videos to share them on the Internet… Moreover, companies all over the world invest a lot of time and money in developing hardware to efficiently multiply arrays. Thus, even minor improvements in the efficiency of matrix multiplication can have a widespread impact.

Strassen’s algorithm

For centuries, mathematicians believed that the standard matrix multiplication algorithm was the best that could be achieved in terms of efficiency. But in 1969, German mathematician Volker Strassen presented a method for multiplying matrices of size two faster than the standard methods known up to that point. Then considered revolutionary, it is still often used today.

By studying very small matrices (size 2×2), Volker Strassen discovered an ingenious way to combine the matrix entries to produce a faster algorithm. More than fifty years later, experts have not found the optimal algorithm for multiplying two 3 × 3 matrices, nor have they managed to outperform Strassen’s two-level approach in a finite body, which AlphaTensor has achieved.

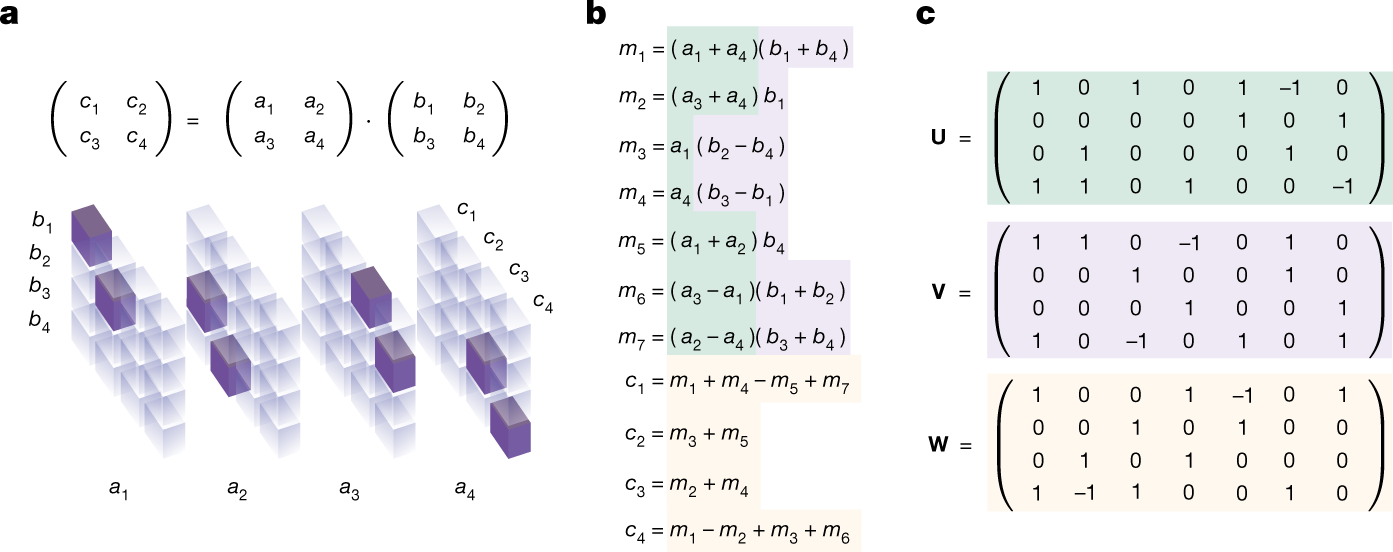
The figure below illustrates a matrix multiplication tensor and algorithms.

The TensorGame

The researchers formulated the procedure for discovering the matrix multiplication algorithm (i.e., the tensor decomposition problem) as a solo game, called TensorGame. In each step of TensorGame, the player selects a combination of different matrix entries to multiply. A score is assigned based on the number of selected operations that achieved the correct multiplication result. According to them, it is a challenging game with a huge action space (more than¹⁰¹² actions for most interesting cases), much larger than that of traditional board games such as chess and Go which have only hundreds of actions.

The AlphaTensor algorithm

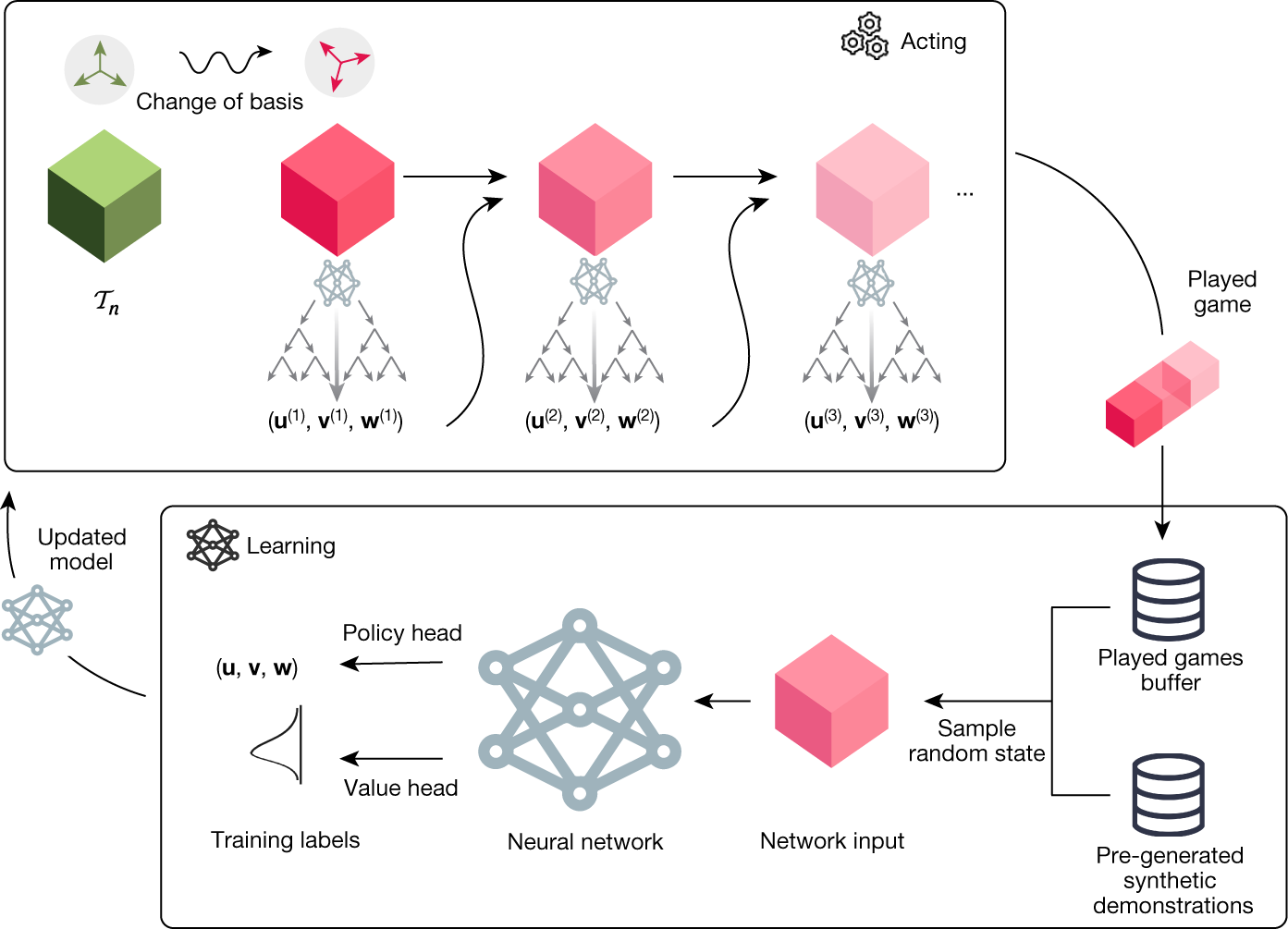
To play TensorGame, they proposed AlphaTensor, an agent based on AlphaZero and its extension to handle large action spaces Sampled AlphaZero. Like AlphaZero, AlphaTensor uses a deep neural network to guide a Monte Carlo Tree Search (MCTS) planning procedure.

The network takes as input a state, i.e. a tensor to be decomposed, and generates a strategy and a value. The strategy provides a distribution over potential actions.

Results

AlphaTensor has discovered algorithms that outperform state-of-the-art complexity for many matrix sizes, including 4 x 4 matrices in a finite body, where it was the 1st to outperform Strassen’s two-level algorithm, indeed it discovered a 47-step solution while Strassen’s had 49 steps.

These algorithms for multiplying small matrices can be used as primitives to multiply much larger matrices of arbitrary size.

AlphaTensor has led to the discovery of a diverse set of algorithms with state-of-the-art complexity: up to thousands of matrix multiplication algorithms for each size, demonstrating that the space of matrix multiplication algorithms is richer than previously thought.

The researchers took advantage of the diversity of different mathematical and practical properties of these algorithms and thus adapted AlphaTensor to specifically find fast algorithms on a given hardware, such as the Nvidia V100 GPU and Google TPU v2.

These multiply large matrices 10-20% faster than commonly used algorithms on the same hardware, highlighting AlphaTensor’s flexibility in optimizing arbitrary objectives.

Article source:

“Discovering faster matrix multiplication algorithms with reinforcement learning”.Nature 610, 47-53 (2022). https://doi.org/10.1038/s41586-022-05172-4

Authors: Alhussein Fawzi, Matej Balog, Aja Huang, Thomas Hubert, Bernardino Romera-Paredes, Mohammadamin Barekatain, Alexander Novikov, Francisco J. R. Ruiz, Julian Schrittwieser, Grzegorz Swirszcz, David Silver, Demis Hassabis & Pushmeet Kohli

Translated from DeepMind accélère la découverte d’algorithmes de multiplication matricielle avec AlphaTensor